State of polarization of the light waves

To benefit fully from this page which contains interactive figures built with the software of geometry GeoplanW and GeospaceW you must give the responsability a page HTML on the site of the CREEM (Experimentation and Research center on the Teaching of Mathematics). On the other hand you do not need this software to read them. To make knowledge with this procedure in addition very fast implement and very light click on the imagette below. You will find all information there on this software and the means of remote loading.

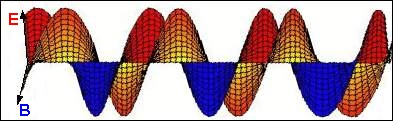
I am sure that you will then be tempted to charge the versions free of this software, well-known of the teachers, and to benefit from their enormous possibilities.

Light waves polarized rectilignement.

The undulatory character of the light was stated for the first time by Huygens in 1678. Work of Fresnel largely developed these ideas by the study of the phenomena of diffraction and interferences. Maxwell in 1876 connected the undulatory character of the light to electromagnetism by writing the equations which the fields check electric and magnetic which are propagated in the vacuum at the same speed as the light. He concludes from it that the light is of nature electromagnetic.
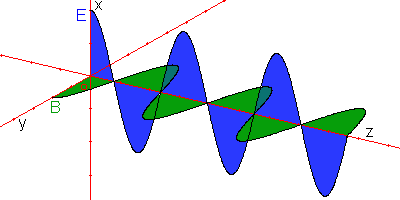
The simplest case is that of a plane wave polarized rectilignement. The vectors electric field E and magnetic field B form with the vector of wave K= w/cn (N vector unit in the direction of the propagation) a trihedron (E, B, K) trirectangular and direct. Each one of these vectors remains in the same plan. The plan defined by E and K is called plane of polarization.

Elliptically and circularly polarized light waves.

The plane light waves are characterized by electric fields and magnetic E and B respectively which one can considérér separately as the sum of two perpendicular fields which are propagated according to the normal direction in the plan which they form.


introducing the delay of phase of E2 compared to E1it comes